Centre of Mass

When the axis of rotation of a body changes does the moment of inertia also change? Why?

What is meant by rigid body?

Two particles of mass $2 \mathrm{g} \mathrm{and} 4 \mathrm{g}$ each are situated at a distance of $6 \mathrm{m}$. This system of masses can be treated as a point mass at a distance of _____$\mathrm{m}$ from the $4 \mathrm{g}$ mass.

The centre of mass of two particles divides internally the line joining them in inverse ratio of their _____.

If the external force is equal to zero on a system then:

Centre of mass of a rigid body is not necessarily the geometric centre of the rigid body.

The centre of mass of a rod will not be at its centre if:

Which of the following statement is always true for a binary star system?

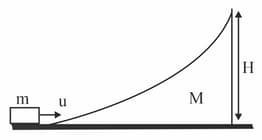
A block of mass $m$ is projected towards a wedge of mass $M$ with a velocity $u$ as shown in the figure below. All the surfaces are smooth. Find the expression for the maximum height attained by the block as it moves on the surface of the wedge.

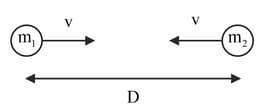
Two masses at a distance equal to $D$ are moving towards each other due to gravitational pull as shown in the figure below. Find the expression for the relative velocity of two masses when the distance between the two masses become $D/2$.

The concept of reduced mass can be used in the problems where the force between the two masses is:

Two masses $m$ and $2m$ are connected by a spring are kept on a frictionless table as shown in the figure below. The block of mass $m$ is imparted the velocity equal to $v$ towards right. Find the maximum compression in the spring.

What do you understand by reduced mass?

The centre of the circular path of all the particles of the rotating body lies on:

All the particles of a rotating rigid body always follow the circular path of the same radius.

All the particles on the axis of rotation are not at rest for:

The axis of rotation of a purely rotating body:

All the particles of a rigid body rotating about its axis, are in translational motion.

The linear speed of a particle A on a body at a distance of $20 \mathrm{cm}$ from its axis of rotation is$40 \mathrm{cm} {\mathrm{s}}^{-1}$ . The body is rotating with a constant angular speed. Find the linear speed and angular speed of particle B at a distance of $40 \mathrm{cm}$ from the axis of rotation.